BioJava:Tutorial:Simple HMMs with BioJava
Tutorial
by David Huen
We will now go through the source of one of the examples in the
demos/dp directory: Dice.java (contributed by Samiul Hasan).
Introduction
The program implements the “occasionally dishonest casino” example used in the book “Biological Sequence Analysis” by R. Durbin, S. Eddy, A. Krogh, G. Mitchison.
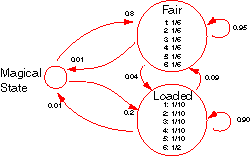
Basically, it conceives a casino with two dice, one fair and one loaded. The fair die lands on any of its sides equal probability while the loaded die yields “6” half the time, all the other sides being of equal probability. These probabilities represent the emission distribution of the fair die state and the loaded die states respectively.
The casino switches between using the fair die and the loaded die periodically. When on the fair die, the probability that the next throw is with the fair die too is 0.95. Similarly, when on the loaded die, the probability of continuing with it is 0.90. These probabilities yield the transition distributions of the states.
The HMM as modelled in the code is slightly modified from the above description with the inclusion of a MagicalState. This state is used to represent the start and end of the states of the model. The transition from the MagicalState to the fair die state occurs with a probability of 0.8 while the transition to the loaded die state occurs with a probability of 0.2. A termination condition was also introduced to allow transitions from the fair die and loaded die states to the Magical state with a probability of 0.01.
Code
The core of the program is the createCasino() method. This creates an
instance of the MarkovModel class that implements the model.
public static MarkovModel createCasino() {
Symbol[] rolls=new Symbol[6];
//set up the dice alphabet
SimpleAlphabet diceAlphabet=new SimpleAlphabet();
diceAlphabet.setName("DiceAlphabet");
for(int i=1;i<7;i++) {
try {
rolls[i-1]= AlphabetManager.createSymbol((char)('0'+i),""+i,Annotation.EMPTY_ANNOTATION);
diceAlphabet.addSymbol(rolls[i-1]);
} catch (Exception e) {
throw new NestedError(
e, "Can't create symbols to represent dice rolls"
);
}
}
A Symbol array rolls is created to hold the symbols generated by
AlphabetManager to represent the outcomes of the dice. An alphabet is
also defined over these symbols.
Next, distributions representing the emission probabilities of the
fair die and loaded die states are created (named fairD and loadedD
respectively). The die states themselves are then created as
SimpleEmissionStates, fairS and loadedS respectively.
You will observe an int array advance with a single value of 1. In a
single-head HMM like ours, there is only one generated sequence and in
our case, we progress along this sole sequence a single position per
transition in the model. In multihead HMMs, there will be multiple
sequences generated by the HMM and it is possible that the increment
through the different sequences might be different. For example,
single-stepping a protein sequence amounts to an increment of three on
its corresponding DNA sequence.
int [] advance = { 1 };
Distribution fairD;
Distribution loadedD;
try {
fairD = DistributionFactory.DEFAULT.createDistribution(diceAlphabet);
loadedD = DistributionFactory.DEFAULT.createDistribution(diceAlphabet);
} catch (Exception e) {
throw new NestedError(e, "Can't create distributions");
}
EmissionState fairS = new SimpleEmissionState("fair", Annotation.EMPTY_ANNOTATION, advance, fairD);
EmissionState loadedS = new SimpleEmissionState("loaded", Annotation.EMPTY_ANNOTATION, advance, loadedD);
The HMM is then created with these states:-
SimpleMarkovModel casino = new SimpleMarkovModel(1, diceAlphabet, "Casino");
try {
casino.addState(fairS);
casino.addState(loadedS);
} catch (Exception e) {
throw new NestedError(e, "Can't add states to model");
}
Next, we need to model the transitions between the states. We do this like so:-
try {
casino.createTransition(casino.magicalState(),fairS);
casino.createTransition(casino.magicalState(),loadedS);
casino.createTransition(fairS,casino.magicalState());
casino.createTransition(loadedS,casino.magicalState());
casino.createTransition(fairS,loadedS);
casino.createTransition(loadedS,fairS);
casino.createTransition(fairS,fairS);
casino.createTransition(loadedS,loadedS);
} catch (Exception e) {
throw new NestedError(e, "Can't create transitions");
}
Note the presence of a MagicalState that is returned by
casino.magicalState(). This is inherent to the SimpleMarkovModel
class and does not need to be created by the user.
The emission distributions fairD and loadedD we set up earlier need
to be initialised. We do that here.
try {
for(int i=0;i<rolls.length;i++) {
fairD.setWeight(rolls[i],1.0/6.0);
loadedD.setWeight(rolls[i], 0.1);
}
loadedD.setWeight(rolls[5],0.5);
} catch (Exception e) {
throw new NestedError(e, "Can't set emission probabilities");
}
We also need to initialise the transition distributions. Note how this
is done: the transition distribution of each state is requested from the
model with a getWeights() and then updated with the required values by
calling the getWeight() method of that distribution. It is not
necessary thereafter to call setWeights() to pass the distribution for
a state back to the model. This may seem strange but it is done this way
because model object may use unique Distribution classes that cannot
be replaced by a generic Distribution class for greater internal
efficiency. Every state in the model needs to have its own transition
distribution initialised appropriately.
//set up transition scores.
try {
Distribution dist;
dist = casino.getWeights(casino.magicalState());
dist.setWeight(fairS, 0.8);
dist.setWeight(loadedS, 0.2);
dist = casino.getWeights(fairS);
dist.setWeight(loadedS, 0.04);
dist.setWeight(fairS, 0.95);
dist.setWeight(casino.magicalState(), 0.01);
dist = casino.getWeights(loadedS);
dist.setWeight(fairS, 0.09);
dist.setWeight(loadedS, 0.90);
dist.setWeight(casino.magicalState(), 0.01);
} catch (Exception e) {
throw new NestedError(e, "Can't set transition probabilities");
}
Having completed constructing the MarkovModel, all that remains is to return it to the caller.
return casino;
Using the MarkovModel
Having created the MarkovModel, we create the corresponding dynamic
programming object:-
DP dp=DPFactory.DEFAULT.createDP(casino);
Now, at last, we have something we can use! To generate a sequence of dice throws with this model, we do:-
StatePath obs_rolls = dp.generate(300);
SymbolList roll_sequence = obs_rolls.symbolListForLabel(StatePath.SEQUENCE);
The generate() method generates a path through the model that emits
300 symbols and we turn that path into a SymbolList with the second
line.
At this point, it will be worthwhile digressing briefly on the
StatePath object. This object embodies an Alignment of the sequences
emitted by the DP object. In a multihead object, multiple aligned
sequences will be emitted. In our case, only a single sequence is
emitted and that is accessed with the label StatePath.SEQUENCE. That
sequence turns out to a run of dice throws from our occasionally
dishonest casino.
Next, we want to test one of the DP algorithms in the DP object. We
want to process the roll_sequence SymbolList we have just generated
and use the Viterbi method to predict which die each of the throws might
have arisen from.
To do this, we create an array of SymbolLists with only
roll_sequence in it - ours is a single-head HMM - and apply the
Viterbi algorithm using the model probabilities
(ScoreType.PROBABILITY) for the computation (you could have also
applied the null-model or log-odds probabilities here). This will yield
the state path that has most support from the model and that state path
is the model’s prediction of which die a particular result came from.
SymbolList[] res_array = {roll_sequence};
StatePath v = dp.viterbi(res_array, ScoreType.PROBABILITY);
All that remains is to print out the generated sequence and the actual state path from which it came (ie. which die) and the HMM estimate of the state path, v, (which is which die a particular throw came from as estimated by the HMM).
//print out obs_sequence, output, state symbols.
for(int i = 1; i <= obs_rolls.length()/60; i++) {
for(int j=i*60; j
The first two print statements print the generated sequence and the
actual state path by accessing the obs_rolls StatePath<code> with the
<code>StatePath.SEQUENCE and StatePath.STATES respectively. The
predicted state path comes from the third print block which accesses the
v StatePath.
The output then looks like this:-
544552213525245666363632432522253566166546666666533666543261
fffffffffffflllllllllllfffffffffffflllllllllllllllllllffffff
ffffffffffffffffffffffffffffffffffllllllllllllllllllllffffff
363546253252546524422555242223224344432423341365415551632161
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
144212242323456563652263346116214136666156616666566421456123
fffffflllfffffffffffffffffffffffflfllllllllllllllllfffffffff
fffffffffffffffffffffffffffffffffffllllllllllllllllfffffffff
346313546514332164351242356166641344615135266642261112465663
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
The top line is the sequence emitted by our HMM when we made it generate
300 throws. The next is the state from which the throw came (f-fair
l-loaded, these are the first letters of the labels “fair” and “loaded”
we used when creating the SimpleEmissionState objects that represent
the dice). The last is similar but this time from the StatePath v that
is the result of the Viterbi algorithm. The performance is pretty on
this occasion but it can vary widely!